Module Multiprocessing de Python
L'un des objectifs du projet était de paralléliser les étapes d'échantillonnage et d'intégration numérique par une approche de type multiprocessing. Il existe un module natif de Python qui permet de mettre en œuvre une solution multiprocessing. Il s'agit du module Multiprocessing et notamment de sa classe Process, qui consiste à assigner des tâches à un processeur donné. Il est cependant à la charge de l'utilisateur de répartir les tâches sur les différents processeurs.
Parallélisation du module Ray Tracing
Le module Ray Tracing est en charge de l'échantillonnage des points sur les surfaces de la géométrie du modèle à étudier. Cet échantillonnage est réalisé à l'aide d'un algorithme MCRT. Cet algorithme effectue d'abord un échantillonnage uniforme de points sur une sphère construite autour de la géométrie. Puis, le module doit réaliser le suivi des rayons au départ de des points sur la sphère englobante. C'est une partie extrêmement coûteuse en temps de calcul.
Pour augmenter les performances du code la parallélisation de cette étape a donc été réalisée, à l'aide du module de multiprocessing de Python. Concrètement, la sphère englobante est divisée en autant de partie que le nombre de processeurs souhaité, puis chacune des partie est attribuée à un processeur unique.
L'accès à la mémoire partagée est l'une des contraintes qu'il a été le plus difficile à gérer. En l'occurrence, le but recherché est de minimiser autant que possible ce type d'accès mémoire afin d'atteindre une performance maximale. Finalement, la méthode de parallélisation multiprocessing de Python a démontré son efficacité. En effet, le temps de synchronisation des différents processeurs reste bien plus faible que le temps d'exécution global. L'équilibre de charge entre les processeurs est ainsi validé.
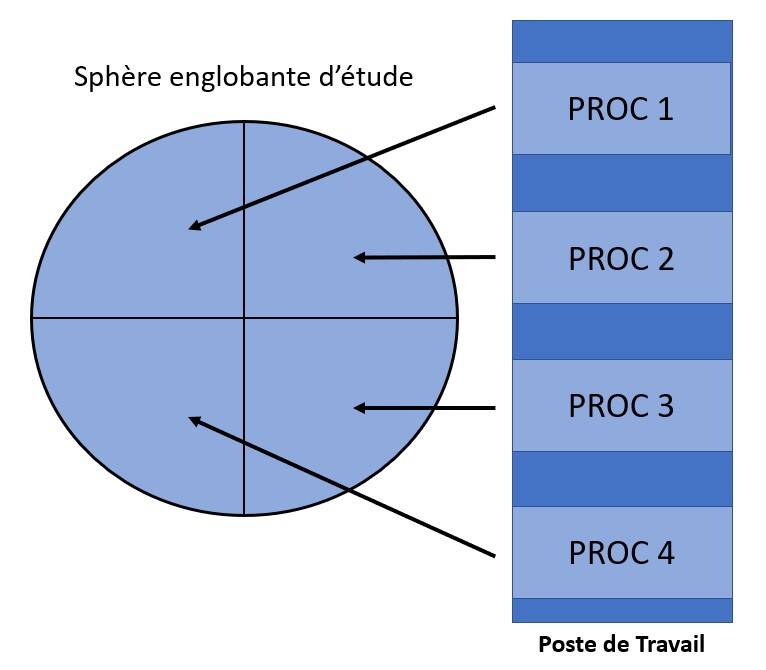
Figure 3. Schéma de la répartition de la charge sur les process.
Parallélisation du module d'intégration
Le module Integration réalise l'intégration numérique permettant de calculer les facteurs de vue du transfert radiatif pour chaque surface de la géométrie. Cette intégration numérique est aussi effectuée à l'aide d'un algorithme MCRT.
Dans cette étape du programme, une hémisphère unitaire centrée est tracée sur une surface cible. Puis l'intégration est réalisée sur les points de discrétisation au sein de cette hémisphère. Pour paralléliser ce calcul, celle-ci est séparée et distribuée de façon égale entre tous les process. De cette façon, chaque process reçoit le calcul intégral sur une partie du domaine. Puis les résultats sur chacun des process sont finalement additionnés pour obtenir la valeur du facteur de vue. L'opération est répétée sur l'ensemble des surfaces cibles.
Créez votre propre site internet avec Webador